AI Gomoku
In this AI gomoku game, we need to design our own heuristic function to calculate the current game, and try to make the best move to win over the opponent. The main way of playing gomoku is to scan the board and use minimax or alpha-beta pruning to predict the move which have the highest score among all the possible moves to beat the opponent.
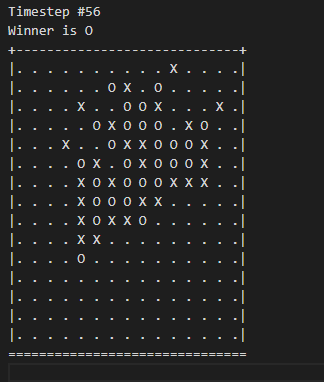
Minimax or alpha-beta pruning is actually not difficult. It is just to build a tree for predicting all of possible steps and try out all the possibilities to find the move with the highest chance of winning. To be able to beat others, the key lies in the search depth of the prediction tree and the design of the heuristic function. The deeper the alpha-beta pruning or minimax are, the more steps it can predict, but also consume more time and memory space. Due to the limitation of memory space and time, it is necessary to try many times to find the deepest depth within the limit. But this is often not the most important point because as long as other opponents have the same level of hardware, they also have the opportunity to reach or even exceed our search depth, so what is the key? Heuristic function!
In this AI, I adopted alpha-beta pruning to reduce the time complexity. For the major heuristic function, I studied every type of terms in gomoku, from the winning five pieces to the winning chess game, to live four, dead four, live three, and so on. This method is called TSS (Threat Space Search), which is a winning method of gomoku researched by Dr. L.V. Allis in 1994. Among the different gomoku patterns, live four and five pieces provide 2 threats, while dead four and live three each provide a threat. Whenever you get 2 threats, you win. So our goal is to get 2 threats. For the rest of patterns, they are calculated by how many connected pieces and empty spaces on the line. The more piece are connected or more the more live chess can be placed, the higher the score will be.
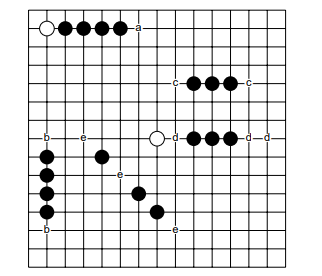
The implementation is to read-in the plate first, then build a tree with a specified search depth, search through by alpha-beta pruning, and finally entering the heuristic function. I use enumerate to search every vertical row, horizontal row, and diagonal row on the chessboard. In each row, I first achieve O(n) threat pattern search through strstr function, and then check the number of connected pieces one by one from the beginning. The score of this row is determined by the number of live chess pieces of each pattern, and the score of the game is obtained by adding and subtracting the scores of both sides. The correct rate of such a heuristic function has a certain degree of accuracy, but the time complexity is too worse. For a 15×15 chessboard, the number of searches for one side is already very considerable, not even talk about the enemy side. It is really a huge burden to calculate the score of both sides, and entering the multi-layer prediction tree of alpha-beta pruning will costs more. Because of the tragedy on the time complexity of the heuristic function, the search depth can only be set to 2 ~ 3 levels, that's really terrible (X.